ПРИМЕНЕНИЕ ГРАФИЧЕСКОГО ПРОЦЕССОРА ПК ДЛЯ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ
П. В. Шаршавин
ООО НПП «Автономные аэрокосмические системы – ГеоСервис»
Институт инженерной физики и радиоэлектроники ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск
Показана возможность реализации операций цифровой обработки сигналов на графическом процессоре ПК на примере нерекурсивного цифрового фильтра, рассмотрены преимущества и недостатки предлагаемых структур фильтров, реализован один из предложенных вариантов построения КИХ-фильтра, измерено время исполнения.
Широкое распространение программно-определяемых радиосистем накладывает дополнительные требования к вычислительным устройствам. По этой причине, в большей части аппаратуры подобных систем, в настоящее время, применяются программируемые логические интегральные схемы (ПЛИС) как самые производительные вычислительные устройства. Необходимая скорость обработки достигается за счет параллельного выполнения операций. Однако главный недостаток ПЛИС – специфичность и сложность разработки программного обеспечения – ограничивает области их применения, устанавливает для разработчиков высокий порог вхождения. Существующие программные продукты генерации прошивки ПЛИС, такие как Xilinx System Generator, на сегодняшний день не позволяют генерировать эффективный код без применения готовых шаблонов модулей. Центральный процессор ПК (CPU) заметно уступает в производительности ПЛИС, зачастую не отвечая современным требованиям по цифровой обработке сигналов. В отличие от него, современный графический процессор (GPU) содержит в себе множество вычислительных ядер, которые могут исполнять практически полный набор инструкций центрального процессора. Пиковая производительность существующих видеокарт может сравниться с производительностью суперкомпьютеров предыдущих поколений.
Таким образом, графический процессор сочетает в себе преимущества центрального процессора (легкость программирования и исполнения) и ПЛИС (параллельность вычислений). Кроме того, цифровая обработка изображений, выполняемая на видеокарте, во многом схожа с цифровой обработкой сигналов, поэтому некоторые специальные инструкции, заложенные в графический процессор для цифровой обработки изображений, применимы и для ЦОС.
До недавнего времени не существовало удобных инструментов доступа к вычислительным ресурсам графического процессора. Однако, в настоящее время активно разрабатывается и развивается технология GPGPU – платформа для программирования с использованием вычислительных ресурсов видеокарты. Существует несколько реализаций технологии GPGPU: NVIDIA CUDA, AMD FireStream, Microsoft Direct Compute и OpenCL. С точки зрения применения графических процессоров в радиоэлектронной аппаратуре, наибольший интерес представляет технология OpenCL, которая является открытой, активно развивающейся, масштабируемой платформой гетерогенных вычислений, позволяющая запускать вычислительные приложения на центральном процессоре, видеопроцессоре, вычислительном кластере, а также на ПЛИС. Остальные реализации GPGPU не представляют практического интереса ввиду их закрытости и ограниченности применения.
Целью данной статьи является демонстрация эффективности применения графических процессоров для задач цифровой обработки сигналов в программно-определяемых радиосистемах, на примере нерекурсивного цифрового фильтра.
OpenCL представляет собой платформу программирования приложений, предоставляющую пользователю специальный язык программирования, основанный на C99, а также различные уровни абстракции. Программа OpenCL, называемая ядром, запускается на так называемых рабочих элементах и рабочих группах, которые ответствуют вычислительным ядрам и группам вычислительных ядер графического процессора [1]. Следует отметить, что в вычислительной системе, содержащей высокопроизводительный графический процессор, узким местом является системная шина, через которую происходит обмен данными и передача команд между центральным и графическим процессором.
Задача реализации нерекурсивного фильтра на графическом процессоре сводится к задаче распараллеливания вычислительных операций в процедуре фильтрации. Прямая форма реализации КИХ-фильтра предполагает последовательное выполнение операций умножения с накоплением и сдвига сигнальной памяти, поэтому не может быть эффективно реализована на параллельной вычислительной платформе.
Для распараллеливания вычислений более подходит транспонированная форма цифрового фильтра [2] за счет отсутствия последовательного суммирования выходов перемножителей элементов фильтра. Структурная схема варианта реализации КИХ-фильтра на основе транспонированной формы приведена на рис. 1. Каждое звено данного фильтра запускается на отдельном рабочем элементе, где последовательно производятся операции умножения на весовой коэффициент, сложения и сдвига сигнальной памяти.
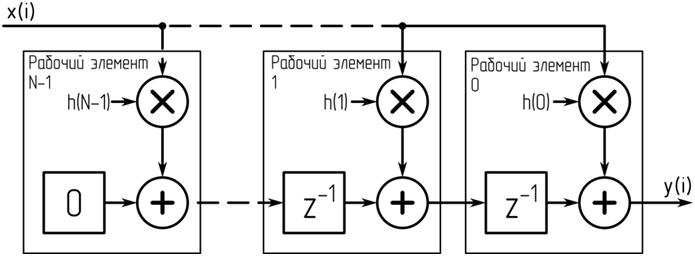
Рис. 1 – Структурная схема реализации КИХ-фильтра с параллельной обработкой по элементам структуры на основе транспонированной формы
Достоинством такой схемы является полностью параллельная обработка по отсчету сигнала. Данное достоинство имеет вес в применении параллельной обработки в реальном времени. Также необходимо отметить, что имеющиеся аппаратные возможности современных графических процессоров позволяют объединить операции умножения и сложения в одной команде. Таким образом, в идеальном случае, для выполнения обработки одного отсчета сигнала, рабочим элементам необходимо выполнить две инструкции – умножение со сложением и загрузка выходного отсчета соседнего рабочего элемента.
К недостатку предлагаемой схемы следует отнести необходимость синхронизации рабочих элементов вследствие наличия связи между звеньями через элементы сигнальной памяти. Данный недостаток особенно сильно влияет на скорость вычислений в случае, когда количество рабочих элементов оказывается меньше порядка фильтра: некоторые рабочие элементы после завершения своей части обработки будут находиться в ожидании завершения вычислений других рабочих элементов. Также недостатком является отсутствие параллельности обработки по нескольким отсчетам сигнала – невозможен запуск нескольких копий фильтра на группах рабочих элементов для одновременной обработки нескольких отсчетов сигнала, по причине наличия в структуре внутренней сигнальной памяти, требующей последовательный проход по отсчетам сигнала. Данный недостаток может иметь принципиальное значение в случае необходимости реализации постобработки и блочной обработки сигнала – реализация последовательного цикла обработки требует дополнительной синхронизации всех вычислителей при переходе между отсчетами сигнала, что отрицательно сказывается на скорости обработки.
Как было указано ранее, возможности видеопроцессора по последовательной обработке отсчетов сигнала в реальном времени ограничены характеристиками системной шиной, по которой происходит передача данных между центральным процессором и видеокартой. Для достижения большой производительности, целесообразно производить блочную обработку сигнала. В этом случае обмен по системной шине происходит большими блоками данных, увеличивая эффективную пропускную способность шины. Для блочной обработки сигнала и постобработки, более эффективным оказывается построение цифрового фильтра с параллельностью вычислений по отсчетам сигнала, а не элементам фильтра (рис. 2). Эффективность данной структуры обосновывается большей длиной сигнала в сравнении с длиной импульсной характеристики, и, как следствие, более равномерной нагрузкой на рабочие элементы. Отсутствие внутренней сигнальной памяти, роль которой выполняет сигнальный буфер, позволяет реализовать полностью асинхронную работу рабочих элементов.
К недостатку данной структуры можно отнести наличие последовательных вычислений по элементам фильтра. Данный недостаток отчасти можно устранить, реализовав параллельное умножение. Последовательной операцией в этом случае остается только суммирование.
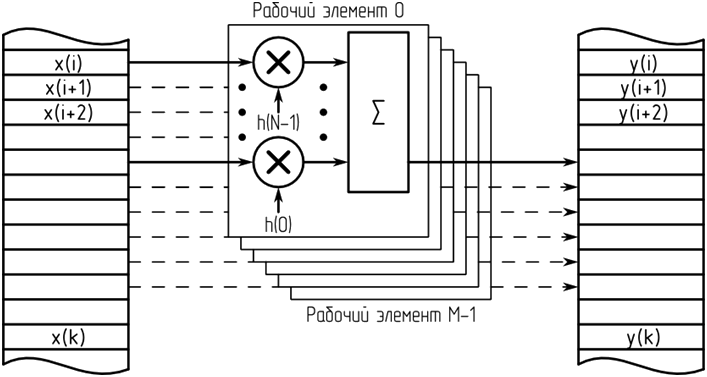
Рис. 2 – Структурная схема реализации КИХ-фильтра с параллельной обработкой по отсчетам сигнала
Для оценки быстродействия выполнения параллельной обработки, реализована структура КИХ-фильтра с параллельной обработкой по отсчетам сигнала на языке OpenCL. Для сравнения с параллельной обработкой, также реализована прямая форма КИХ-фильтра без сдвига сигнальной памяти [3] в последовательном коде на языке программирования C.
Данные реализации фильтров запускались на вычислительной машине со следующими характеристиками:
- центральный процессор – AMD PhenomII X6 1100T, 6 ядер, 3,2 ГГц;
- графический процессор – AMD Radeon HD 6850, 960 ядер, 256-разрядная шина памяти, тактовая частота процессора/шины памяти – 800 МГц/1 ГГц, пиковая производительность – 1,488 Терафлопс;
- тип/объем оперативной памяти – DDR3-1600/8 Гбайт, тип/объем видеопамяти – GDDR5/1 Гбайт;
- операционная система – Ubuntu 12.10 (ядро Linux 3.5.0), 64-разрядная;
- компилятор – GCC 4.7.2.
Синтез импульсной характеристики производился в пакете MATLAB sptool. Для эксперимента синтезированы полосовые фильтры со следующими значениями порядка: 10, 50, 100, 1000. В качестве тестовых сигналов использовались дельта-импульс и гармоническое колебание на центральной частоте фильтра. Длина сигнала составляет 5•104 и 107 отсчетов. Фильтры работают с числами с плавающей точкой одинарной точности, неприменение чисел с плавающей точкой двойной точности обусловлено отсутствием их поддержки в данной модели графического процессора. Измерение времени обработки производится функцией clock_gettime стандартной библиотеки time.h языка C. Для каждого порядка фильтра и длины сигнала, процедуры обработки и измерения времени выполнения запускаются 1000 раз, полученный массив измерений подвергается статистической обработке путем построения гистограммы и вычисления среднего значения времени выполнения.
Результаты статистической обработки результатов измерений (средние значения) сведены в табл.1, а также показаны в виде графиков на рис. 3,4.
Таблица 1. Время обработки сигнала на центральном и графическом процессорах
| Длина сигнала | 5x104 | ||||
| Порядок фильтра | Время обработки, мс | Время обработки на один элемент, нс | Выигрыш | ||
| CPU | GPU | CPU | GPU | ||
| 10 | 0,836 | 3,418 | 1,672 | 6,836 | 0,245 |
| 50 | 3,885 | 3,786 | 1,554 | 1,515 | 1,026 |
| 100 | 7,320 | 4,064 | 1,464 | 0,813 | 1,801 |
| 1000 | 138,922 | 13,580 | 2,778 | 0,272 | 10,230 |
| Длина сигнала | 5x107 | ||||
| Порядок фильтра | Время обработки, мс | Время обработки на один элемент, нс | Выигрыш | ||
| CPU | GPU | CPU | GPU | ||
| 10 | 0,166 | 0,043 | 1,663 | 0,425 | 3,908 |
| 50 | 0,762 | 0,079 | 1,524 | 0,157 | 9,704 |
| 100 | 1,443 | 0,123 | 1,443 | 0,123 | 11,779 |
| 1000 | 27,246 | 1,735 | 2,725 | 0,173 | 15,705 |
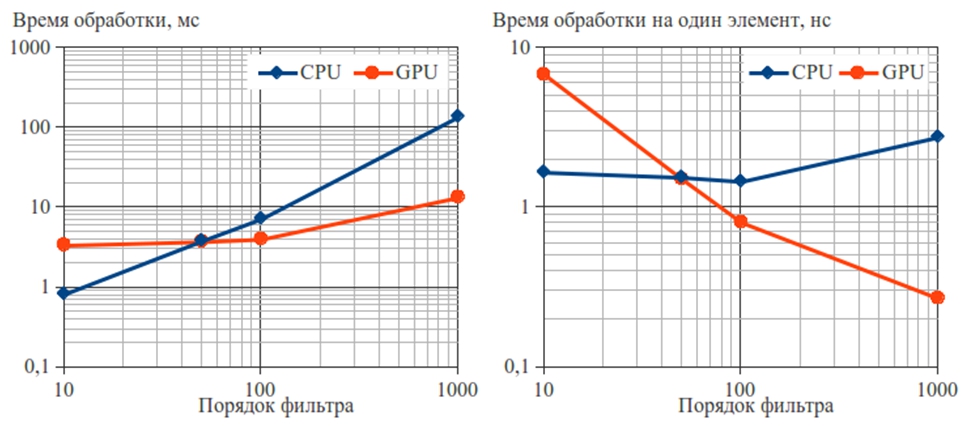
Рис. 3. Время обработки сигнала на центральном и графическом процессорах для длины сигнала 5•104
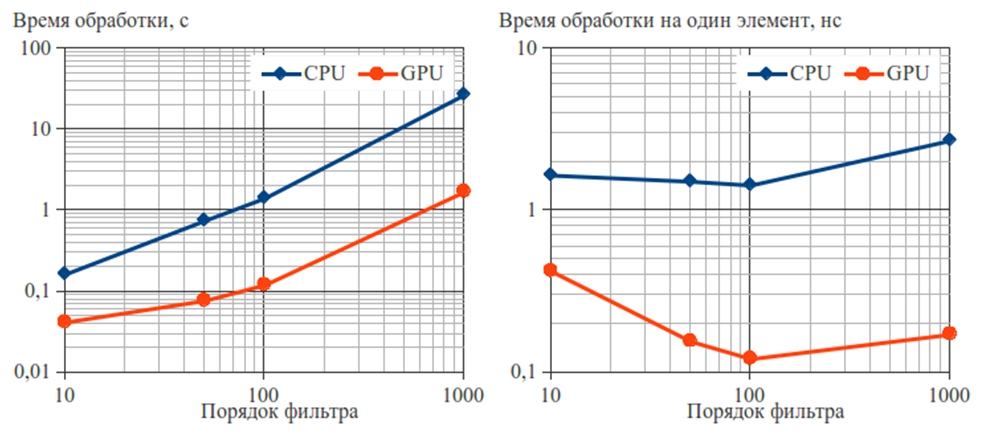
Рис. 4. Время обработки сигнала на центральном и графическом процессорах для длины сигнала 107
Как показано на графиках и в таблице, преимущества графического процессора перед центральным в скорости обработки проявляются уже при порядках фильтра, превышающих 50, достигая 15,7-кратного выигрыша при максимальной длине сигнала и порядке фильтра, для которых проведен эксперимент. Падение производительности вычислений на графическом процессоре при малых порядках фильтра и длинах сигнала обусловлено большой нагрузкой на системную шину, через которую в этом случае пересылаются малые порции данных с большой частотой. Время обработки на один элемент в центральном процессоре практически не зависит от длины сигнала и порядка фильтра.
На примере нерекурсивного фильтра показана эффективность применения графических процессоров для цифровой обработки сигналов. Следует отметить, что данный выигрыш не является пределом – показан лишь простейший пример. Путем оптимизации и применения специальных приемов и схем построения блоков ЦОС, производительность вычислений может быть приближена к пиковой для графического процессора. Полученные результаты имеют особую ценность в задачах цифровой регистрации и программной постобработки, а также обработки в реальном времени сигналов спутниковых радионавигационных систем. Наличие внутри ПК столь мощного вычислительного устройства позволяет реализовать сложные алгоритмы высокоточных измерений координат в программной постобработке и в блочной обработке в реальном времени.
Работа выполнена при поддержке Министерства образования и науки Российской Федерации.
СПИСОК ЛИТЕРАТУРЫ
1. The OpenCL Specification: Version 1.2, Document Revision 19 / Khronos OpenCL Working Group, 2012. – 308 с.
URL: http://www.khronos.org/registry/cl/specs/opencl-1.2.pdf (дата обращения: 25.02.2013).
2. Сергиенко А.Б. Цифровая обработка сигналов: учеб.пособие, 3-е изд. / А.Б.Сергиенко. — СПб.: БХВ-Петербург, 2011. – 768с.: ил. – ISBN 978-5-9775-0606-9
3. Глинченко А.С. Цифровая обработка сигналов: учеб.пособие, 2-е изд., перераб. и доп. / А.С.Глинченко – Красноярск: ИПЦ КГТУ, 2005. – 482c.
660079, Россия, г. Красноярск,
ул. Электриков, 156/1


