ИССЛЕДОВАНИЕ МЕТОДА ПОСТОБРАБОТКИ СИГНАЛОВ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ С ПОВЫШЕНИЕМ ЧАСТОТЫ ДИСКРЕТИЗАЦИИ
П. В. Шаршавин, А. В. Гребенников (научный руководитель)
ООО НПП «Автономные аэрокосмические системы – ГеоСервис»
Институт инженерной физики и радиоэлектроники ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск
Рассмотрена проблема ограничения частоты дискретизации при обработке навигационных сигналов. Предложен метод высокоскоростной постобработки для повышения точности оценок параметров сигналов, разработана математическая модель. Получены экспериментальные зависимости погрешностей измерения задержки ПСП от отношения сигнал/шум.
Программная постобработка навигационных сигналов является приложением так называемой цифровой регистрации. Идея метода заключается в постобработке ранее принятого, оцифрованного и записанного на носитель информации навигационного сигнала. Устройство, реализующее данный метод (рисунок 1) состоит из цифрового регистратора и персональной ЭВМ со специализированным программным обеспечением.
С помощью постобработки могут быть решены проблемы, которые трудно, либо невозможно решить современными методами обработки сигналов в реальном масштабе времени [1]. Одной из таких проблем является повышение точности оценки параметров навигационного сигнала, в частности, задержки ПСП.
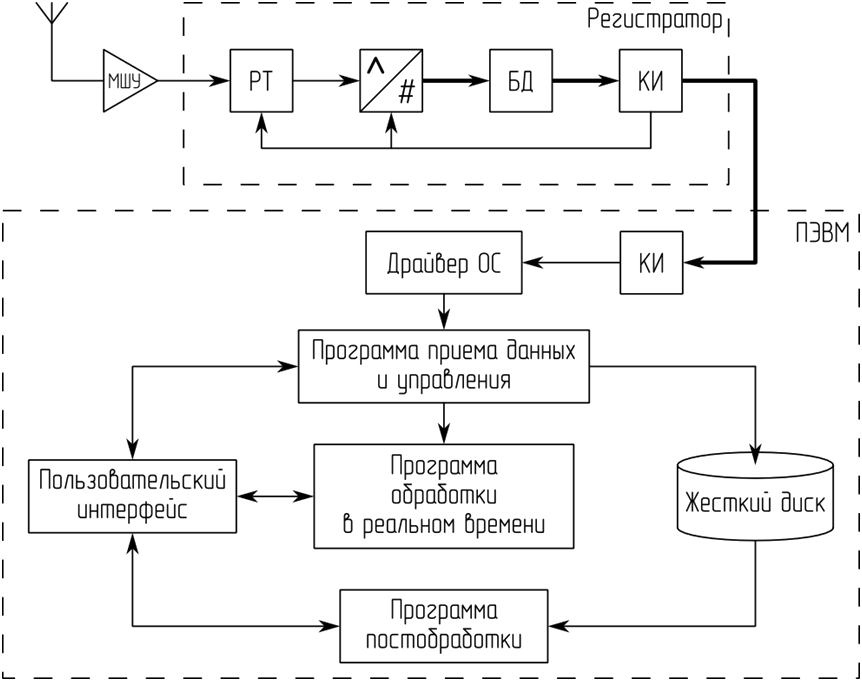
Рисунок 1. Структурная схема программного приемника:
МШУ – малошумящий усилитель; РТ – радиотракт; БД – буфер данных; КИ – контроллер интерфейса; ПЭВМ – персональная ЭВМ.
Одной из необходимых мер повышения точности оценки задержки ПСП является уменьшение погрешностей дискретизации входного сигнала и опорной ПСП коррелятора. Следствием погрешности дискретизации является возникновение запаздывания дискретного сигнала относительно непрерывного в процессе дискретизации (рисунок 2а). Запаздывание имеет равномерный закон распределения с максимальным значением погрешности, равным периоду дискретизации (рисунок 2б) [2]. Очевидно, ее максимальная величина обратно пропорциональна частоте дискретизации. Поскольку классический подход обработки в реальном времени предполагает обработку сигналов на частоте дискретизации АЦП, выборки опорной ПСП генерируются синхронно с отсчетами входного сигнала, и опорная ПСП также имеет погрешность дискретизации.
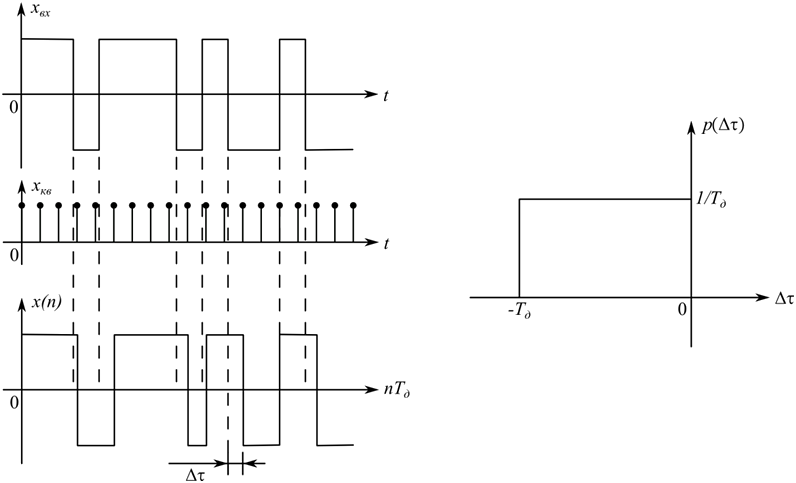
Рисунок 2. Погрешность дискретизации опорной ПСП коррелятора:
а – процесс дискретизации; б – график распределения плотности вероятности погрешности.
Из методов уменьшения погрешности дискретизации, наиболее часто применяется метод повышения частоты дискретизации АЦП. Эффективность данного метода ограничивается аппаратными возможностями современных АЦП, а также аппаратными возможностями устройств цифровой обработки сигналов.
Применение постобработки позволяет значительно уменьшить влияние данных ограничений. В частности, это дает возможность осуществлять обработку сигнала с высокой частотой дискретизации, выше частоты дискретизации АЦП. Данная возможность позволяет уменьшить погрешность дискретизации опорной ПСП коррелятора пропорционально увеличению частоты дискретизации. Для согласования частот дискретизации входного сигнала и опорной ПСП предлагается вместо прореживания выборок опорной ПСП повысить частоту дискретизации входного сигнала с помощью интерполяции.
Блок цифровой обработки, реализующий данный принцип (рисунок 3) отличается от применяемого при обработке в реальном времени наличием экспандера частоты дискретизации входного сигнала и фильтра-интерполятора [3]. Также в блоке отсутствуют элементы понижения частоты дискретизации опорной ПСП. Соответственно, коррелятор работает на высокой частоте дискретизации, что позволяет повысить точность оценки псевдодальности. Недостатком данного решения являются большие вычислительные затраты. Однако, этот недостаток не является существенным, поскольку обработка не осуществляется в реальном времени.
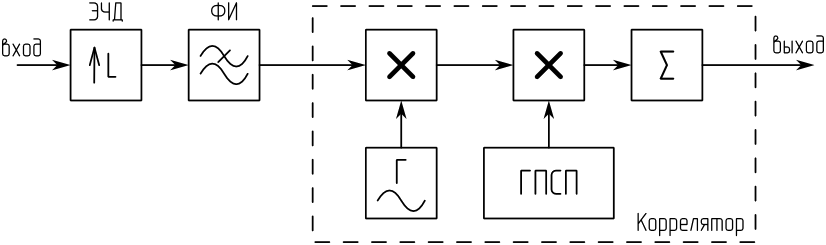
Рисунок 3. Структурная схема коррелятора программного приемника с повышением частоты дискретизации:
ЭЧД – экспандер частоты дискретизации; ФИ – фильтр-интерполятор; ГПСП – генератор псевдослучайной последовательности.
Для исследования предложенного метода разработана математическая модель, состоящая из генератора навигационных сигналов и корреляционного приемника.
Генератор навигационных сигналов формирует навигационный сигнал с дальномерным кодом на промежуточной частоте (рисунок 4). Генератор ПСП формирует М-последовательность, либо коды Голда, в зависимости от выбранной навигационной системы. Частота дискретизации ГПСП задается пользователем. При передискретизации ПСП на эту частоту, учитывается заданный доплеровский сдвиг частоты путем корректировки коэффициента передискретизации. Перенос на промежуточную частоту и доплеровский сдвиг частоты реализованы раздельно. Полоса пропускания полосового фильтра также может быть задана пользователем. Элемент задержки состоит из двух блоков – блок задержки на целое число отсчётов с помощью простого сдвига отсчётов, а также блок задержки на дробное количество отсчётов, реализованный на фильтре Фарроу третьего порядка. Таким образом, задержка может быть задана произвольно, и, в процессе моделирования, задается случайным числом с равномерным распределением в диапазоне от 0 до 1 мс. Генератор шума (ГШ) формирует аддитивный белый гауссов шум, дециматор уменьшает частоту дискретизации сигнала до требуемой для моделирования. Точность установки задержки сигнала, в основном, определяется свойствами используемого фильтра Фарроу, а также точностью вычисления коэффициентов передискретизации при формировании ПСП.
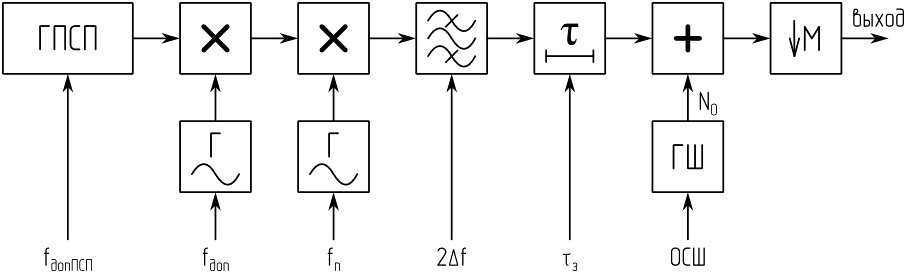
Рисунок 4. Структура математической модели генератора навигационных сигналов
Модель корреляционного приемника (рисунок 5) состоит из экспандера частоты дискретизации, фильтра-интерполятора и квадратурного коррелятора. Экспандер частоты дискретизации и фильтр-интерполятор выполняют повышение частоты дискретизации и сглаживание получившихся отсчетов, что является ключевой особенностью предлагаемого метода. Коррелятор выполняет вычисление модуля ВКФ с помощью простого перебора задержки опорной ПСП. Измерение задержки ПСП производится по максимуму ВКФ.
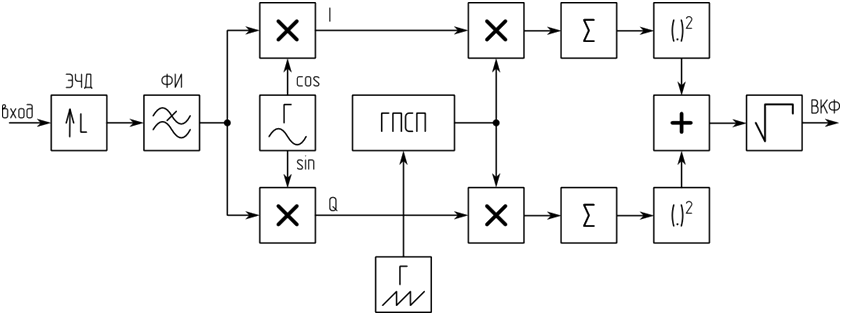
Рисунок 5. Структура математической модели корреляционного приёмника с повышением частоты дискретизации
На рисунке 6 приведены полученные в результате моделирования зависимости статистических характеристик погрешностей измерения задержки ПСП от отношения сигнал/шум для различных методов обработки: при частотах дискретизации 10 и 100 МГц без интерполяции, а также при частоте дискретизации 10 МГц с повышением до 100 МГц с интерполяцией нулевого порядка и линейной интерполяцией. Ширина полосы навигационного сигнала, задаваемая полосовым фильтром генератора (см. рисунок 4) составляет 4 МГц, время накопления в корреляторе – 10 мс. Доплеровский сдвиг частоты принят равным нулю. Для каждого значения отношения сигнал/шум выполнено 1000 итераций моделирования.
По результатам моделирования можно сделать следующие выводы:
- оценка задержки ПСП не является смещенной для любого из методов измерения;
- методы оценки задержки ПСП с использованием интерполяции по своим точностным характеристикам занимают промежуточное положение между прямыми измерениями на низкой и высокой частотах дискретизации.;
- среднеквадратичное значение погрешности оценки задержки в методах с использованием интерполяции при малых значениях отношения сигнал/шум асимптотически стремится к соответствующим значениям, полученным при измерениях на низкой частоте дискретизации. При высоких отношениях сигнал/шум, а также при отсутствии шума, значение СКО погрешности близко к значению СКО для высокой частоты дискретизации;
- СКО погрешности оценки задержки для метода измерения с применением линейной интерполяции оказывается несколько меньше СКО погрешности метода с интерполяцией нулевого порядка;
- оценка задержки ПСП для системы GPS при малых значениях отношения сигнал/шум точнее аналогичной для системы ГЛОНАСС.
Для реального навигационного сигнала в полосе 2Δf = 4 МГц при спектральной плотности мощности шума N0 = -200 дБВт/Гц и мощности сигнала P = -160 дБВт отношение сигнал/шум составляет:
ОСШ= P/(2∆fN0)=-160 дБВт-(10 lg(4∙106Гц)-200 дБВт/Гц)=-26 дБ.
Выигрыш в СКО погрешности оценки задержки ПСП для метода с интерполяцией относительно метода без повышения частоты дискретизации (см. рисунок 6) для данного значения отношения сигнал/шум составляет 10 нс для ГЛОНАСС СТ и 15 нс для GPS C/A. Данный выигрыш может иметь значение в специальных навигационных приложениях, поскольку улучшается точность измерения еще до вторичной обработки сигнала.
В задачах применения беззапросных измерительных станций, благодаря специальным мерам, как правило, отношение сигнал/шум оказывается больше рассчитанного выше. Поэтому выигрыш предлагаемого метода может оказаться весьма значительным.
Наконец в задачах поверки имитаторов навигационных сигналов, где возможна работа на сильном сигнале, методы с интерполяцией позволяют получить статистические характеристики погрешностей измерения задержки ПСП, эквивалентные получаемым на высокой частоте дискретизации без интерполяции.
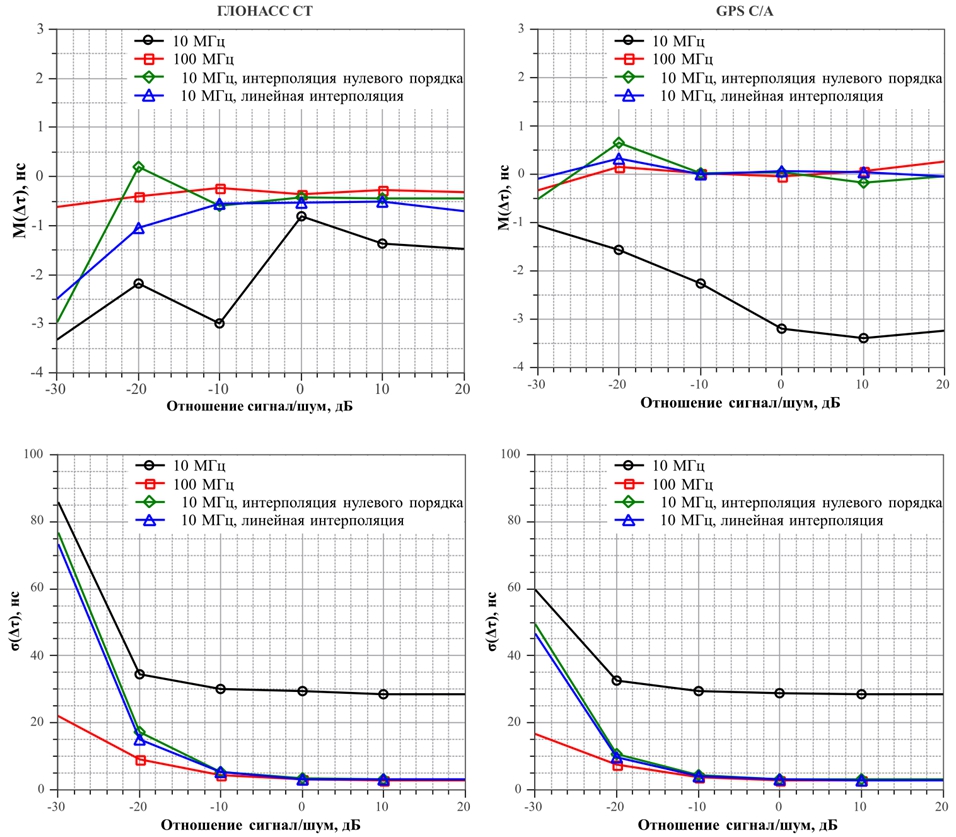
Рисунок 6. Экспериментальные зависимости статистических характеристик погрешностей измерения псевдодальности от отношения сигнал/шум
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Шаршавин П. В., Сизасов С. В., Гребенников А. Г. Программная постобработка и программные приемники навигационных сигналов СРНС ГЛОНАСС/GPS : Современные проблемы радиоэлектроники : сб. науч. тр. / науч. ред. Г. Я. Шайдуров. Красноярск :Сиб. федер. Ун-т, 2011.
2. Мирский Г. Я. Электронные измерения : 4-е изд., перераб. и доп. М. : Радио и связь, 1986.
3. Глинченко А. С. Цифровая обработка сигналов : учеб.пособие. 2-е изд., перераб. и доп. Красноярск : ИПЦ КГТУ, 2005.
660079, Россия, г. Красноярск,
ул. Электриков, 156/1


