СИНХРОНИЗАЦИЯ ЦИФРОВЫХ СИСТЕМ СВЯЗИ ПО СИГНАЛАМ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ

Н. М. Боев

ООО НПП «Автономные аэрокосмические системы – ГеоСервис»

Институт инженерной физики и радиоэлектроники ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск boev@uav-siberia.com

 

Большинство современных цифровых систем радиосвязи имеют несколько систем синхронизации, которые располагаются на приемной части радиосистемы.

 

Среди них выделяют:

• системы синхронизации по несущей частоте (ССН);
• системы тактовой синхронизации (СТС);
• системы словной синхронизации (ССС);
• системы кадровой синхронизации (СКС).

В первую очередь выполняется синхронизация по несущей частоте, затем по тактовой частоте, по словной частоте и по кадровой частоте.

 

Для каждой системы синхронизации выделяют два режима работы: режим вхождения в синхронизм (режим поиска); режим слежения. В режиме вхождения в синхронизм осуществляется поиск и обнаружение сигнала, грубая оценка его неизвестных параметров. После чего система захватывает сигнал и переходит в режим слежения, в котором осуществляется точная оценка неизвестных параметров принимаемого сигнала. Переход в синхронный режим может осуществляться при помощи информации, передаваемой в начале сеанса связи или по самому информационному сигналу. Таким образом, эффективность передачи полезных данных снижается из-за затрат на передачу данных, необходимых только для синхронизации и необходимого времени для поиска сигнала и перехода в режим слежения всех систем синхронизации приемника [1]. В связи с этим не теряют актуальности вопросы повышения эффективности работы систем синхронизации.

 

Одним из методов синхронизации передающего и приемного устройств является принудительная синхронизация с использованием всемирного точного времени [2]. В этом случае метки точного времени на концах линии передачи данных формируются, например, при помощи приемников глобальных спутниковых радионавигационных систем (СРНС) ГЛОНАСС/GPS/Galileo. Современные приемные устройства СРНС способны синхронизировать временные шкалы пользователя с погрешностью в десятки наносекунд и лучше, что позволяет использовать их для синхронизации цифровых систем связи по несущей частоте.

 

Предлагается следующая структурная схема синхронизации передающего и приемного устройств по сигналам спутниковых навигационных систем (рисунок 1).

 

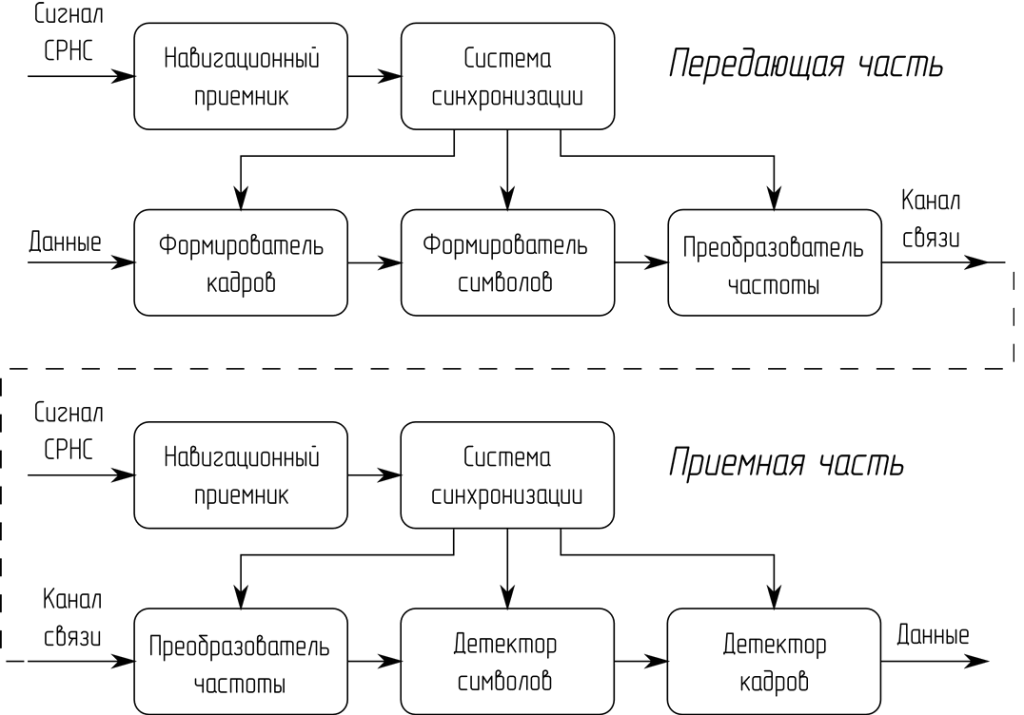
Рисунок 1 – Структурная схема синхронизированной системы связи

 

Навигационные приемники передающей и приемной части системы связи служат для определения координат местоположения устройств и синхронизации шкал времени. Определение координат местоположения устройств позволяет вычислить расстояние между передатчиком и приемником системы связи, рассчитать и учесть задержку на распространение сигнала (другим способом определения этой задержки является способ автоматической калибровки, когда передатчик излучает в определенные моменты времени сигнал-маркер, а приемник производит оценку задержки этого сигнала по всемирной шкале времени).

 

Кроме того, при связи с движущимися объектами, приемник СРНС выдает данные о векторе скорости объекта, что позволяет учесть в системе синхронизации эффект Доплера.

 

Отличительными особенностями предлагаемого варианта синхронизации являются:

• реализация синхронизации цифровых систем связи по несущей частоте;
  
• создание возможности построения систем связи без каких-либо дополнительных петель синхронизации;
  
• реализация возможности использования шкалы всемирного времени для синхронной смены параметров программно-определяемых систем связи.
  

Использование приемников СРНС для синхронизации шкал времени передатчика и приемника позволяет обеспечить синхронизацию с определенной погрешностью. В общем случае ухудшение работы системы передачи данных, вызванное ошибками синхронизации, зависит от выбранного вида модуляции. Для определения степени влияния ошибок синхронизации шкал времени приемника и передатчика цифровой системы связи были реализованы соответствующие модели в программе Simulink [3].

 

Общий вид модели приемопередающего устройства в Simulink показан на рисунке 2.

   

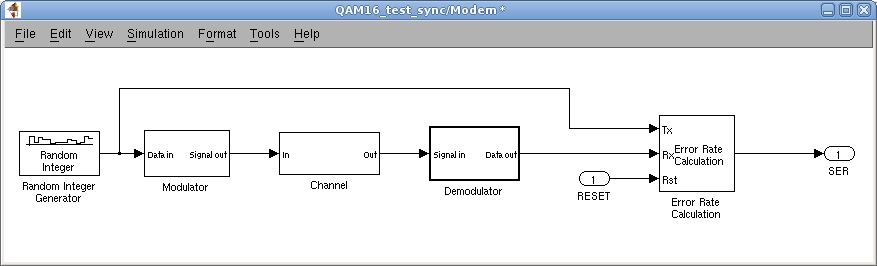
Рисунок 2 – Модель приемопередатчика в Simulink

 

Данные для формирователя комплексной огибающей сигнала (рисунок 3 и 4) формируются генератором случайных чисел (рисунок 2, Random Integer Generator).

 

   

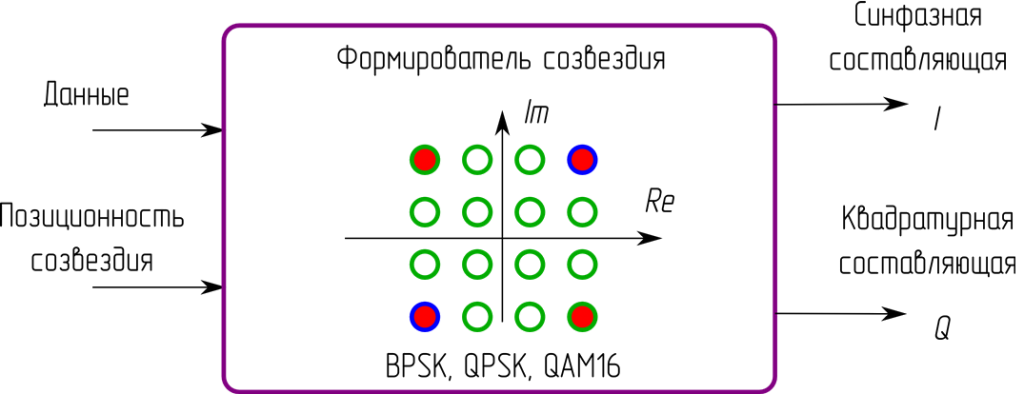
Рисунок 3 – Формирователь комплексной огибающей сигнала

 

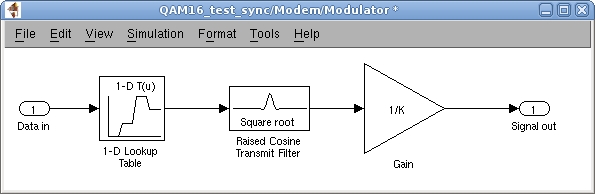
Рисунок 4 – Формирователь комплексной огибающей сигнала в Simulink

 

Сформированный сигнал поступает в канал (рисунки 5 и 6), в котором осуществляется моделирование следующих явлений:

• воздействия аддитивного белого гауссова шума;
• частотного и фазового сдвига сигнала вследствие эффекта Доплера и рассогласования шкал времени приемника и передатчика;
• дробной задержки в канале связи;
• замираний сигнала.

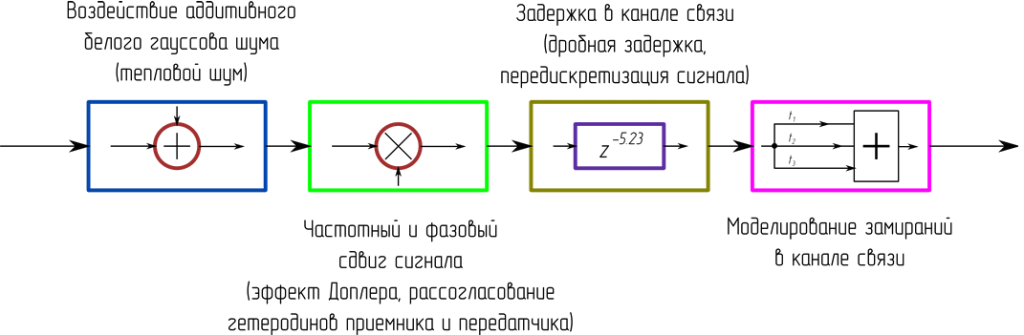
Рисунок 5 – Моделирование канала связи

 

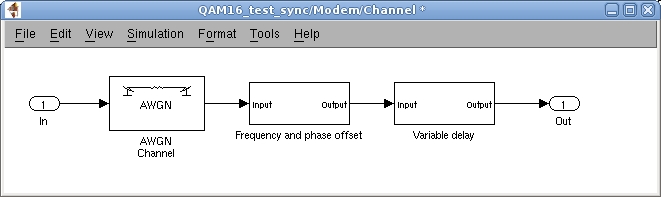
Рисунок 6 – Модель канала связи в Simulink (без моделирования замираний)

 

Приемная часть системы в базовом виде содержит петлю восстановления несущего колебания (петля с возведением сигнала в квадрат, синфазно-квадратурная петля и др.) и петлю восстановления тактовых импульсов (например, петля Гарднера) (рисунок 7).

   

 

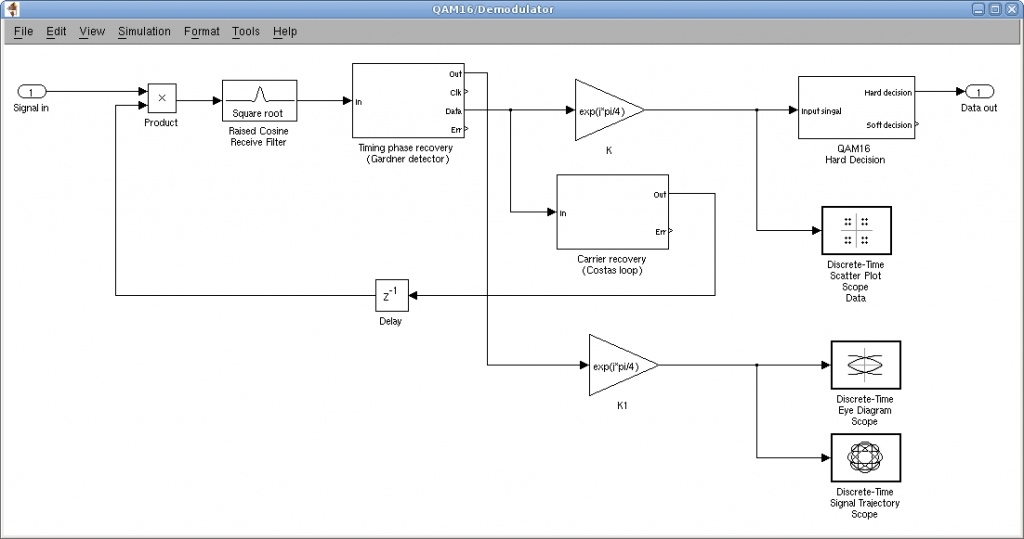
Рисунок 7 – Модель приемника в Simulink с петлями синхронизации по несущей и по символьной частоте

 

Демодуляция принятого сигнала осуществляется по результатам расчета метрик (рисунок 8).

 

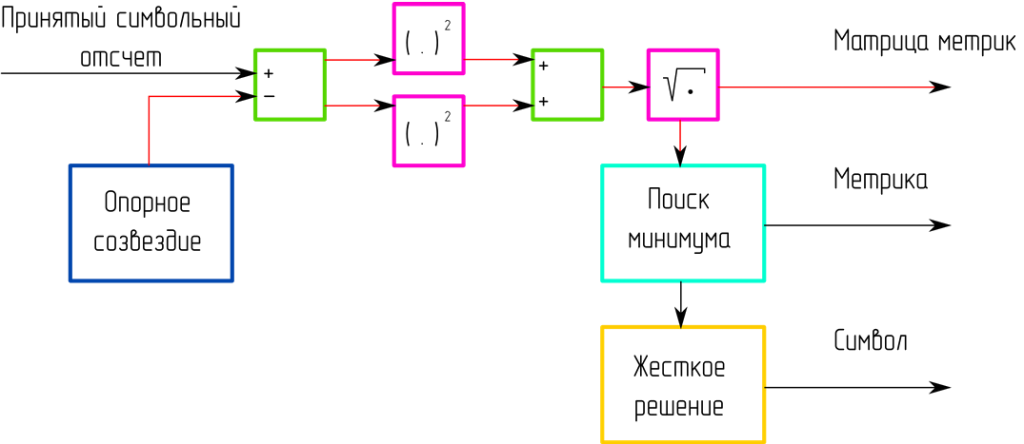
Рисунок 8 – Расчет метрик и демодуляция сигнала

 

На рисунке 9 показана модель демодулятора (рисунок 8) в Simulink.

 

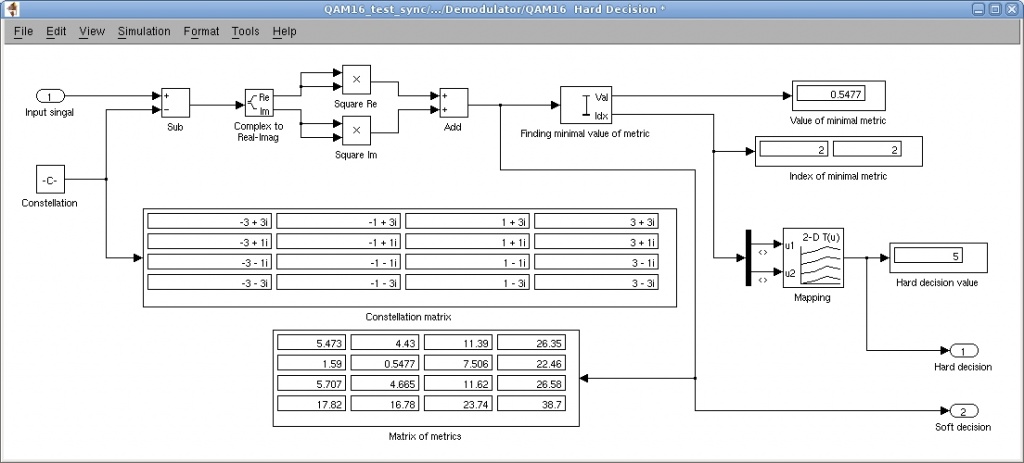
Рисунок 9 – Расчет метрик и демодуляция сигнала в Simulink

 

Для моделирования принудительной синхронизации передатчика и приемника из приемной части системы связи удаляются петля слежения за фазой и частотой сигнала и петля восстановления тактовых импульсов (рисунок 10), что значительно упрощает структуру приемника.

 

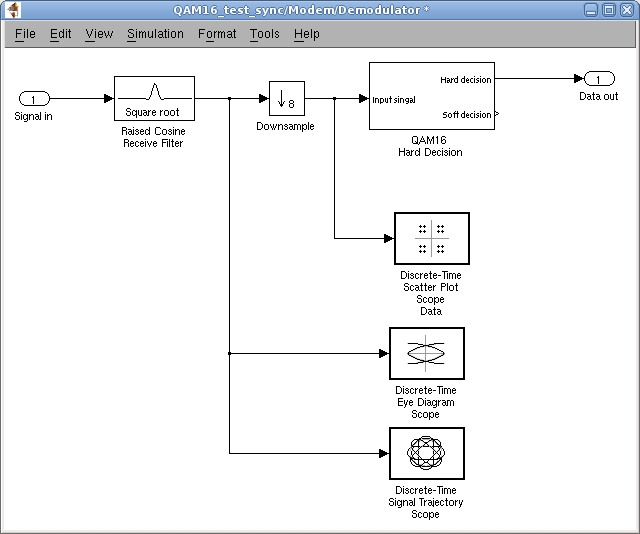
Рисунок 10 – Модель приемника в Simulink без петель синхронизации

 

Перейдем к результатам моделирования.

 

На рисунке 11 показаны зависимости вероятности символьной ошибки от отношения сигнал/шум для квадратурной амплитудной манипуляции (КАМ16) при различных сдвигах временных шкал передатчика и приемника (с условием полной компенсации задержки на распространение сигнала). Задержка в канале носит случайный характер с равномерным распределением. Данные зависимости были получены в ходе моделирования и соответствуют теоретическим выкладкам [4].

   

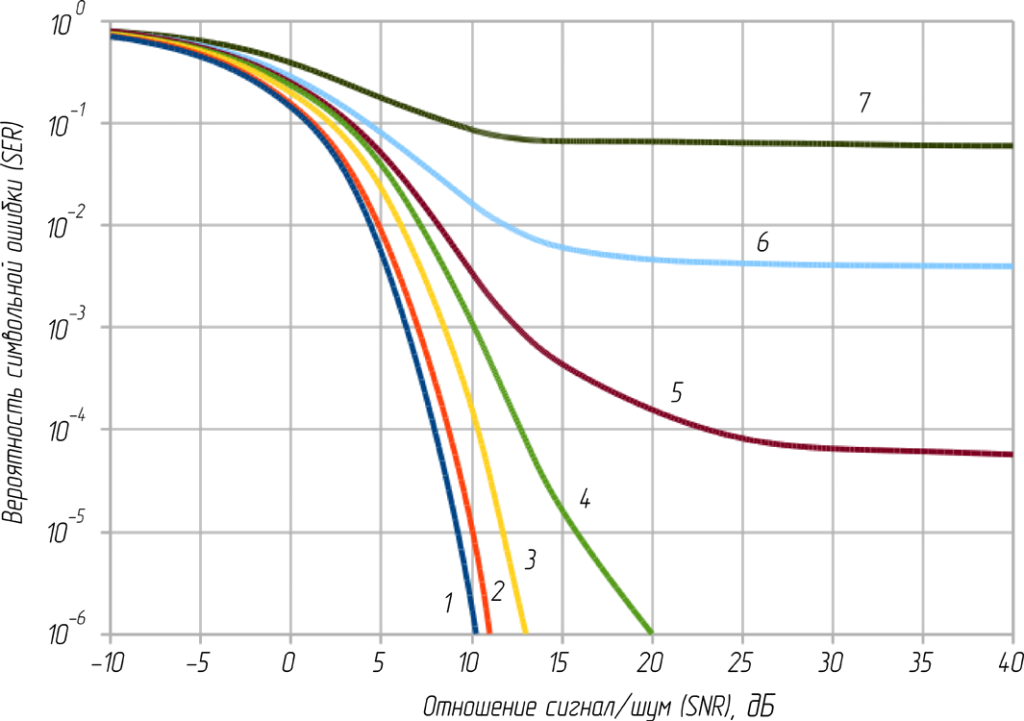
Рисунок 11 – Зависимости вероятности символьной ошибки от отношения сигнал/шум 

при различном сдвиге временных шкал передатчика и приемника для модуляции КАМ16:

1 – ±ΔT = 0; 2 – ±ΔT = Ts/16; 3 – ±ΔT = Ts/8; 4 – ±ΔT = Ts/5;

5 – ±ΔT = Ts/4; 6 – ±ΔT = Ts/3; 7 – ±ΔT = Ts/2

На рисунке 12 приведена экспериментально полученная зависимость разности временных шкал приемников навигационной системы ГЛОНАСС, находящихся на расстоянии 5 км.

   

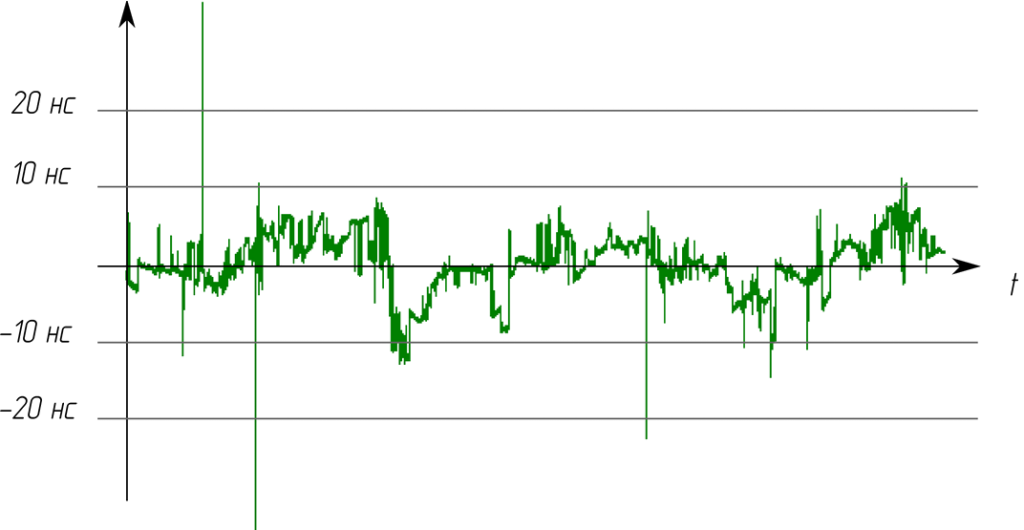
Рисунок 12 – Разность временных шкал двух навигационных приемников ГЛОНАСС за период времени ~11 часов

Таким образом, при ошибке синхронизации до ±10 нс возможна передача данных с периодом следования символов 80 нс. Потери в этом случае составят 3 дБ для вероятности символьной ошибки 10-5 (зависимость 3 на рисунке 11). Увеличение периода следования символов при той же вероятности символьной ошибки в два раза (160 нс) уменьшит потери до 1 дБ (зависимость 2 на рисунке 11), а уменьшение периода следования символов в два раза (40 нс) увеличит потери до 7 дБ (зависимость 4 на рисунке 11).

 

Для тактирования гетеродинов (петель ФАПЧ) преобразователей частоты передатчика и приемника предполагается использование опорной частоты 10 МГц навигационных приемников. При этом возникает ряд проблем, которые приводят к фазовому рассогласованию при приеме сигнала и, как следствие, к повороту сигнального созвездия, что приводит к повышению вероятности ошибки. На рисунке 13 показаны графики зависимостей вероятности символьной ошибки от отношения сигнал/шум при различных дисперсиях фазового шума, распределенного по нормальному закону. При этом ошибка смещения шкал времени лежит в диапазоне ±ΔT = Ts/4./p>

 

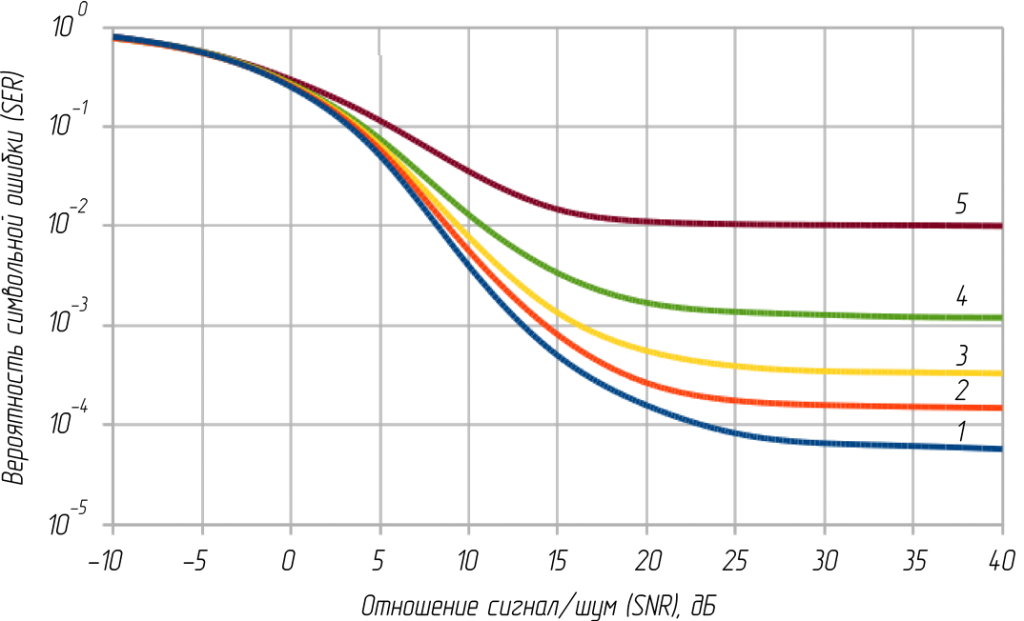
Рисунок 13 – Зависимости вероятностей символьной ошибки от отношения сигнал/шум при различных значениях дисперсии фазового шума и ошибке смещения шкал времени ±ΔT = Ts/4 для модуляции КАМ16: 1 – σ2 = 0; 2 – σ2 = π/8; 3 – σ2 = π/4; 4 – σ2 = π/2; 5 – σ2 = π

Как видно из рисунка 13, одновременная ошибка синхронизации шкал времени и фазовая ошибка приводят к заметному ухудшению работы системы связи. Поэтому в каждом конкретном случае реализации системы связи необходимо учитывать все ошибки синхронизации единовременно и в случае необходимости применять дополнительные меры для их компенсации.

 

Для подтверждения результатов теоретических расчетов и моделирования был поставлен эксперимент. На рисунке 14 показана структурная схема экспериментальной установки.

  

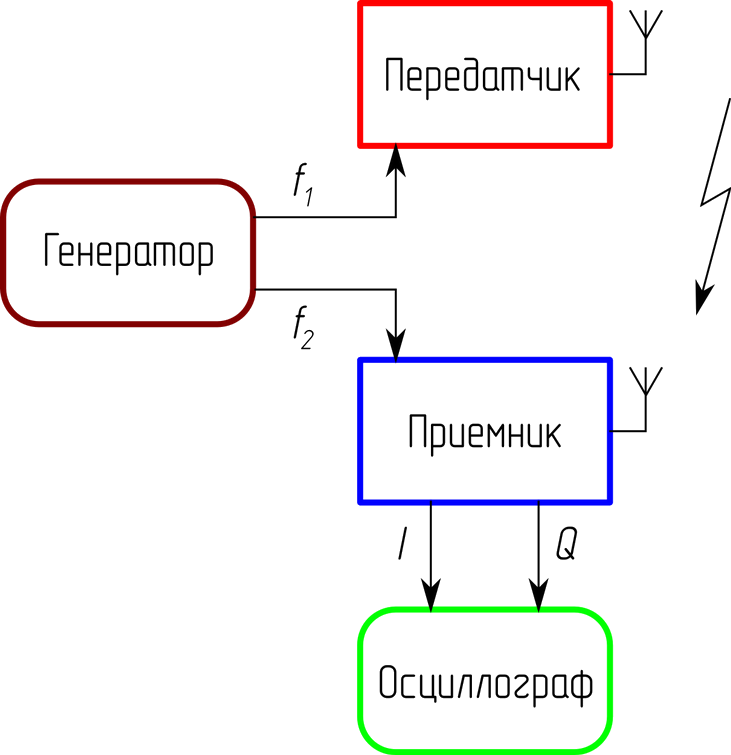
Рисунок 14 – Структурная схема экспериментальной установки

 

Двухканальный генератор прямоугольных импульсов (рисунок 14) формирует опорные колебания для тактирования БЦОС и гетеродинов приемника и передатчика. Использование одного двухканального генератора позволяет формировать два опорных колебания с известным фазовым и частотным рассогласованием. Приемник и передатчик цифровой системы связи работают в штатном режиме, сигнал с выхода преобразователя частоты поступает на двухканальный осциллограф для отображения траектории вектора комплексной огибающей сигнала.

 

На рисунке 15 показана глазковая диаграмма одной из квадратурных составляющих принимаемого сигнала при тактировании передатчика и приемника от одного источника тактовых импульсов.

 

   

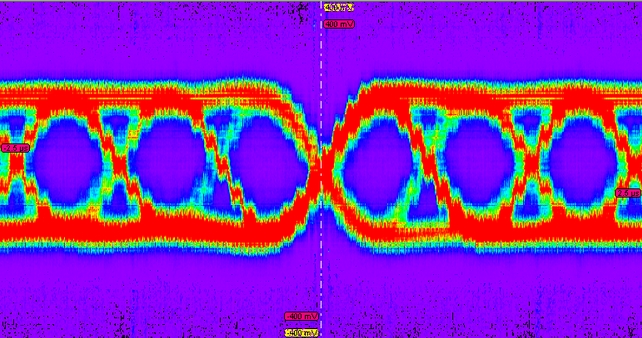
Рисунок 15 – Глазковая диаграмма одной из квадратурных составляющих приемного тракта

 

Заключение

В ходе проведенных испытаний была подтверждена возможность использования радионавигационных систем для синхронизации цифровых систем связи. Анализ полученных в ходе эксперимента данных показал необходимость контролирования начальной фазы синтезатора частот гетеродина. Вследствие асинхронной инициализации синтезаторов частот передатчика и приемника возникает фазовый сдвиг между несущими колебаниями, который приводит к повороту созвездия. Устранить данный фазовый сдвиг можно двумя способами: синхронной синфазной инициализацией синтезаторов частот гетеродинов передатчика и приемника или введением в приемный тракт петли фазовой синхронизации.

 

Синхронизация устройств цифровой связи с использованием приемников СРНС позволяет упростить структуру приемника и значительно сократить затраты на синхронизацию приемного устройства. Работа подобного устройства принудительной синхронизации не зависит от мощности шума на входе приемника, что позволяет исключить зависимость вероятности ошибки от соотношения сигнал/шум, характерную для классических систем синхронизации. В случае, когда полное исключение систем синхронизации невозможно, комплексирование системы связи с навигационной системой позволяет:

• адаптивно изменять параметры петель синхронизации для более быстрого перехода в режим слежения;
• использовать упрощенные системы синхронизации;
• использовать шкалу абсолютного времени для синхронной смены основных параметров радиосистемы (модуляции, кодирования, шифрования и др).

На рисунке 16 показаны условия по необходимому отношению сигнал/шум на входе приемника и относительной ошибке синхронизации временных шкал приемника и передатчика для поддержания вероятности символьной ошибки на заданном уровне (10-3, 10-4 и 10-5 для модуляции КАМ16).

 

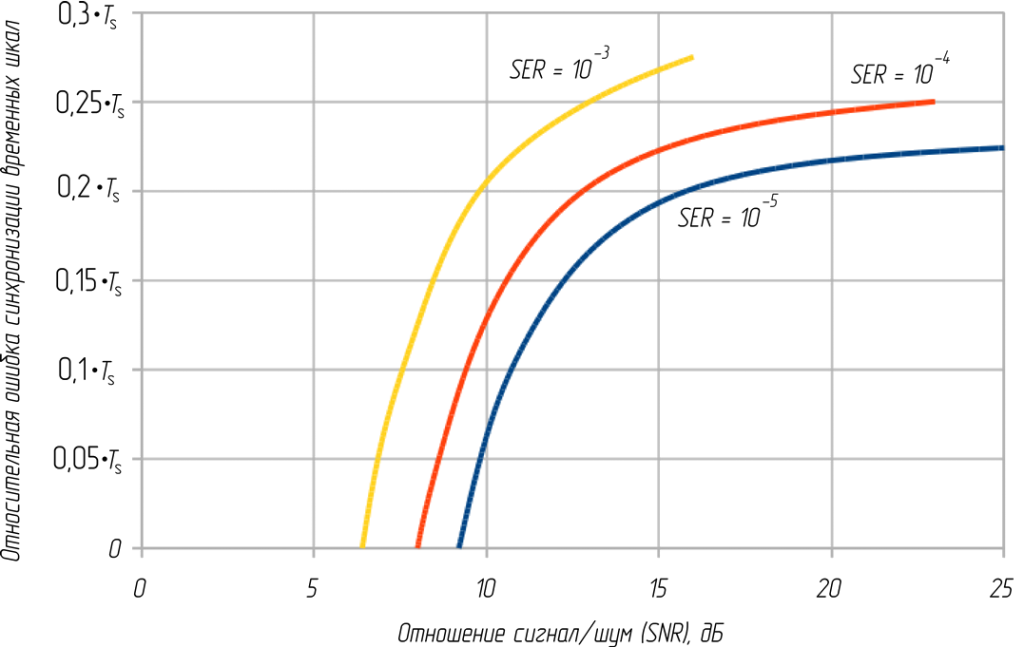
Рисунок 16 – Необходимые условия по относительной ошибке синхронизации временных шкал

приемника и передатчика и отношения сигнал/шум для поддержания вероятности

символьной ошибки на заданном уровне (модуляция КАМ16)

 

В таблицу 1 сведены потери в канале связи для различных скоростей передачи данных при ошибке синхронизации временных шкал 20 нс (рисунок 12) для модуляции КАМ16 и заданной вероятности символьной ошибки 10-5.

   

Таблица 1 – Потери в канале связи, вызванные относительной ошибкой синхронизации временных шкал приемника и передатчика

 

Скорость передачи данных, МБод	Потери, дБ
3,125	1
6,25	3
10	7
Передача с заданной вероятностью символьной ошибки и с более высокой скоростью невозможна	-

Как видно из таблицы 1, современные радионавигационные системы способны обеспечить синхронность работы высокоскоростных цифровых систем передачи данных при приемлемом уровне потерь.

 

Список использованных источников

1. Скляр, Б. Цифровая связь. Теоретические основы и практическое применение, Изд. 2-е, испр.: Пер. с англ. / Б. Скляр. – М.: Издательский дом «Вильямс», 2003. – 1104 c.

2. Прокис, Д. Цифровая связь / Д. Прокис. – М.: Радио и связь, 2000. – 800 c.

3. Simulink. URL: http://www.simulink.com/

4. Mengali, U. Synchronization Techniques for Digital Receivers / U. Mengali, N. D'Andrea. – New York: Plenum Press, 1997. – 524 c.